深度优先搜索(DFS)

顾名思义，深度优先搜素的就在于”深度”二字，通俗来讲，DFS就是从一个起始点开始，找到一个连接点进入
一直进入下去直到没有节点，若找到最后一个节点没有子节点且还存在点没有遍历，则回到上一个节点，继续
寻找节点，直到遍历完所有的点。

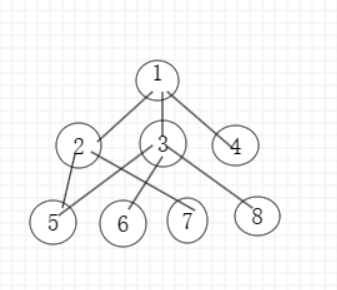
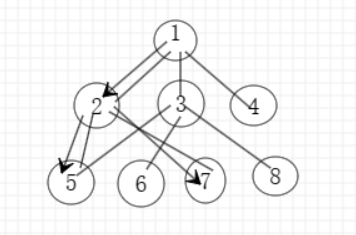
下图是一个无向图：

DFS

如上图所示，从节点1开始遍历，使用DFS算法，节点1有三个子节点，分别为节点2，3，4，因为这里我们没有定义
两个节点之间的距离，所以任意选择下一个节点，这里我们选择先进入节点2,如图所示：

DFS

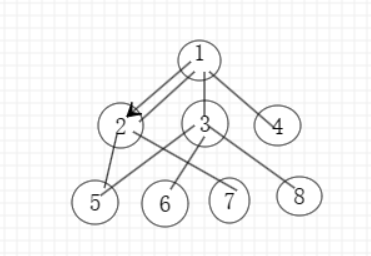
到达节点2之后,与节点2相连的点为1,5,7,但需要注意的是不可能选择节点1,因为节点1已经走过了,所以我们要选择
节点5或者节点7,这里我们选择节点5，如下图所示:

DFS

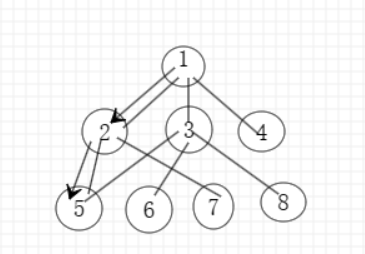
到节点5的时候，发现节点5没有其他相连的节点了,节点2已经记录走过了,所以不能再走节点2。这个时候我们就要进行回溯，
回溯之后，我们又回到节点2，需要注意的是这里的回到节点2，是回到上一步，而不是在走一次节点2，可以理解为”撤回”操作。

这里为了方便理解，在图像里面我用箭头表示，但需要注意的是算法的原理并不是这样，是回溯

如图所示:

DFS

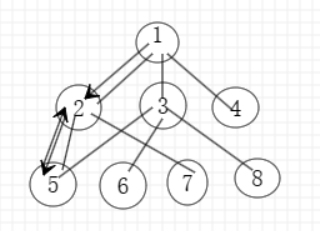
然后我们又回到节点2,继续寻找与节点2并且没有走过的点，可以发现与节点2相连的并且没走过只有节点7，
所以我们接着遍历节点7.如下图所示:

DFS

回到节点7之后,再次没有可遍历的节点，继续回溯到节点2,可以发现在节点2也没有为遍历的节点,就继续回溯到
节点1,然后遍历节点1的其他节点,直到遍历万所有节点，方法过程与前面类似。

实现方法: 根据前面的过程可以发现，先进入的父节点最后才出来,所以这里我们要使用堆(stack)来实现
DFS算法,把存在子节点的父节点添加到堆里面，直到堆为空结束遍历。

广度优先搜索(BFS)

根据前面的DFS的介绍,自然而然可以想到,广度优先搜索则在于广度,即先把起始点的所有节点全部遍历,然后
遍历起始点子节点的节点，流程如下：
BFS

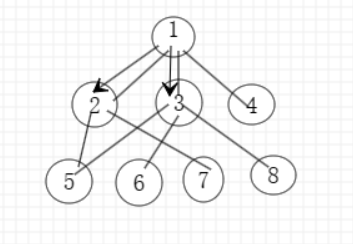
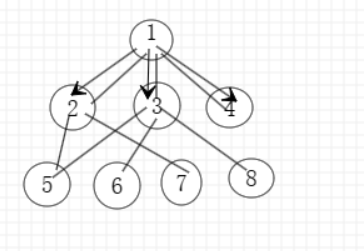
依旧选择节点1为起始点,可以发现节点1的子节点有节点2,3,4。与DFS的不同,BFS会依次遍历节点1的所有节点。
例如我们这里先选择遍历节点2:
BFS

接下来的遍历就与DFS不一样了,我们不会继续按深度遍历下去,而是继续遍历节点1的其他节点:
BFS
BFS

可以发现我遍历节点2后,紧接着遍历的是节点3和节点4,节点1的节点全部遍历完了,紧接这遍历的是节点2的子节点,
因为我们先进入的是节点2,依次类推,直到遍历所有节点。

实现原理: DFS实现用的是堆(Stack),而BFS根据上面的描述可知,是先进先出,节点2在节点3,4之前进入遍历,
那么节点2的子节点就要先于节点3,4的子节点,这里我们使用队列(queue)来实现BFS算法。

下面我们看一个例题来方便我们更深刻理解BFS和DFS两种算法。

迷宫寻路

题目描述

机器猫被困在一个矩形迷宫里。
迷宫可以视为一个 n*m 矩阵，每个位置要么是空地，要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。

机器猫初始时位于 (1, 1)的位置，问能否走到 (n, m) 位置。

输入格式

第一行，两个正整数 n,m。

接下来 n 行，输入这个迷宫。每行输入一个长为 m 的字符串，# 表示墙，. 表示空地。

输出格式

仅一行，一个字符串。如果机器猫能走到 (n, m)，则输出 Yes；否则输出 No。

DFS解法

首先我们选择用DFS算法来解决此问题 ，若使用 dfs 访问(x,y)，若不是终点，则尝试往四个方向中的一个寻找答案。
那么这个 dfs 就可以这么写：

  • 排除非法情况，比如坐标越界和遇到障碍物；
  • 如果访问过，则跳过；
  • 如果没访问过，继续处理并标记已访问；
  • 如果得到答案，退出；
  • 否则向四个方向继续扩展。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>
#include <vector>
using namespace std;

bool dfs(vector<vector<char>>& maze, vector<vector<bool>>& visited, int x, int y, int n, int m) {
    if (x == n && y == m) {
        // 如果当前位置是目标位置，返回true，机器猫可以到达目标位置
        return true;
    }

    visited[x][y] = true; // 标记当前位置为已访问

    // 定义当前位置的上、下、左、右四个相邻位置的偏移量
    vector<pair<int, int>> neighbors = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

    for (auto neighbor : neighbors) {
        int nx = x + neighbor.first;  // 相邻位置的行坐标
        int ny = y + neighbor.second;  // 相邻位置的列坐标

        // 检查相邻位置是否在迷宫范围内、未被访问过，并且是空地（不是墙）
        if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && !visited[nx][ny] && maze[nx][ny] == '.') {
            if (dfs(maze, visited, nx, ny, n, m)) {
                return true;  // 递归调用DFS，如果找到一条路径可以到达目标位置，立即返回true
            }
        }
    }

    return false;  // 当前位置无法到达目标位置
}

bool canReachDestination(vector<vector<char>>& maze) {
    int n = maze.size() - 1;  // 获取迷宫的行数
    int m = maze[0].size() - 1;  // 获取迷宫的列数

    vector<vector<bool>> visited(n + 1, vector<bool>(m + 1, false));  // 记录位置是否已访问的标记矩阵，默认为false

    return dfs(maze, visited, 1, 1, n, m);  // 从起始位置开始进行DFS
    }

    int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<char>> maze(n + 1, vector<char>(m + 1));

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> maze[i][j];
        }
    }

    if (canReachDestination(maze)) {
        cout << "Yes" << endl;
    } else {
        cout << "No" << endl;
    }

    return 0;
}

BFS解法

使用广度优先搜索就要使用到队列，存储待访问的点。
所以我们的 bfs 可以这么写：

  • 把起始点(1,1)入队；
  • 如果队列非空：
    • 弹出队首(x,y)； 判断(x,y) 是否非法，若非法，跳过；
    • 通过堆x,y进行上下左右移动,把(x,y) 相邻的点入队；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

bool canReachDestination(vector<vector<char>>& maze) {
int n = maze.size() - 1;  // 获取迷宫的行数
int m = maze[0].size() - 1;  // 获取迷宫
vector<vector<bool>> visited(n + 1, vector<bool>(m + 1, false));  // 记录位置是否已访问的标记矩阵，默认为false
    visited[1][1] = true;  // 起始位置已访问

    queue<pair<int, int>> q;  // 创建一个队列用于BFS
    q.push({1, 1});  // 将起始位置加入队列

    while (!q.empty()) {
        int x = q.front().first;  // 当前位置的行坐标
        int y = q.front().second;  // 当前位置的列坐标
        q.pop();  // 弹出队首元素

        if (x == n && y == m) {
            // 如果当前位置是目标位置，返回true，机器猫可以到达目标位置
            return true;
        }

        vector<pair<int, int>> neighbors = {{x - 1, y}, {x + 1, y}, {x, y - 1}, {x, y + 1}};
        // 定义当前位置的上、下、左、右四个相邻位置

        for (auto neighbor : neighbors) {
            int nx = neighbor.first;  // 相邻位置的行坐标
            int ny = neighbor.second;  // 相邻位置的列坐标

            // 检查相邻位置是否在迷宫范围内、未被访问过，并且是空地（不是墙）
            if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && !visited[nx][ny] && maze[nx][ny] == '.') {
                q.push({nx, ny});  // 将相邻位置加入队列
                visited[nx][ny] = true;  // 标记相邻位置为已访问
            }
        }
    }

    // 循环结束时仍未返回，表示无法从起始位置到达目标位置
    return false;
}

int main() {
int n, m;
cin >> n >> m;
vector<vector<char>> maze(n + 1, vector<char>(m + 1
for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> maze[i][j];
        }
    }

if (canReachDestination(maze)) 
    cout << "Yes" << endl;
else 
    cout << "No" << endl;
return 0;}

若代码和讲解存在问题，请帮我纠正，谢谢！！