二分查找

二分查找又叫折半查找,需要注意的是二分查找需要数列是有序的,如果查找到需要的数,返回所在位置
,否则返回NULL。

如一个升序长度为7的数组a[7]，分别为1，2，3，4，5，6，7，如下图:
数组序列
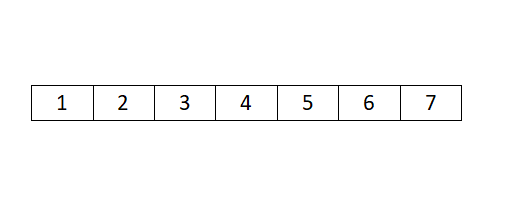
如果查找大小为5的值所在的位置，过程如下：
首先设置两个变量，分别为left = 0，right = 6，left这个参数表示左边端点，right表示右边端点，
因为数组的下表是从0开始的，所以right = 6。
步骤一
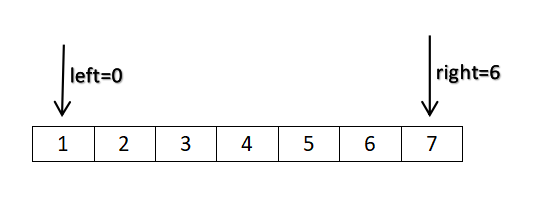
然后开始查找，查找left，right的平均值mid，即mid=(left + right)/2,然后把a[mid]与需要查找
的值5比较，若a[mid] < 5，则太小了，修改left的值，让left = mid + 1；若a[mid] >　5,则表明
查找的数值过大，这是right = mid - 1；若a[mid] = 5，则说明此时的mid即使5在数组中的位置。
所以第一次查找的mid =(0+6)/2= 3,a[mid] = a[3] = 4 < 5,更新left = mid+1。此时left和right
的位置如下图所示：
步骤二
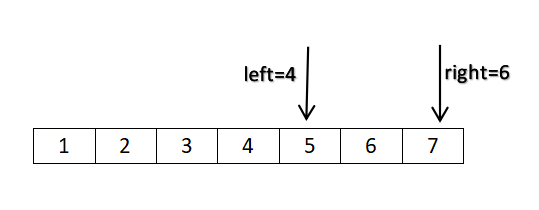
第二次查找mid=(4+6)/2=5,a[mid]=a[5]=6 > 5,更新right = mid - 1。更新后的left和
right如下图所示：
步骤三
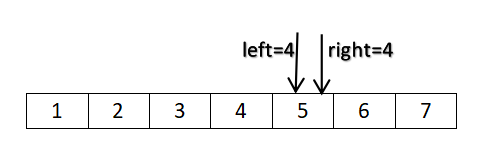
第三次查找mid=(4+4)/2=4,a[mid]=a[4]=5,与查找值相等,停止查找,返回位置4。

实战演练

进击的奶牛

题目描述

Farmer John 建造了一个有 N（2<=N<=10 ^ 5) 个隔间的牛棚，这些隔间分布在一条直线上，坐标是
x1, x2,… xN（0<=xi<=10 ^ 9）。

他的 C（2<=C<=N）头牛不满于隔间的位置分布，它们为牛棚里其他的牛的存在而愤怒。为了防止牛之间的
互相打斗，Farmer John 想把这些牛安置在指定的隔间，所有牛中相邻两头的最近距离越大越好。那么，
这个最大的最近距离是多少呢？

输入格式

第 1 行：两个用空格隔开的数字 N 和 C。

第 2 ~ N+1 行：每行一个整数，表示每个隔间的坐标。

思路：

从题目就可以看的出来这是一个明显的二分问题，我们只需要处理每个每个牛所在的位置与前一个牛的位置距离
差是否满足某个条件，这里需要满足a[i+1] - a[i] >= mid,如果满足这样的个数大于等于C，我们就认为
此时的距离mid可以实现，那样就要增大mid，即向右区间移动，left = mid + 1，不满足则减小mid的值，
向左区间移动，即right=mid-1。最后比较每次的mid求得最大值。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;
int n,m;
int ans=-1;
int a[1000005];
bool check(int x){   //答案是否满足，满足返回1，反之返回0
    int now = 1, num = 1;
    for (int i = 2; i <= n; i++){
        if (a[i]-a[now]>=x){
            now=i;
            num++;
        }
    }
    return num>=m;
}
void merge(int l,int r){
	if(r-l<0) return;    //边界
	int mid=l+(r-l)/2;    //这样处理防止溢出
	if(check(mid)){   //如果满足，我们记录当前最大值，然后往右区间寻找答案
		merge(mid+1,r);
		ans=max(ans,mid);
	}
	else{  //如果不满足，就往左区间寻找
		merge(l,mid-1);
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	sort(a+1,a+n+1);  //输入是无序的，要排序处理。
	merge(1,a[n]-a[1]);
	cout<<ans;
    return 0;
}

紧接着，我们再来看另一题：

砍树

题目描述

伐木工人 Mirko 需要砍 M 米长的木材。对 Mirko 来说这是很简单的工作， 因为他有一个漂亮的新伐木机，可以如野火一般砍伐森林。
不过，Mirko 只被允许砍伐一排树。

Mirko 的伐木机工作流程如下：Mirko 设置一个高度参数 H（米），伐木机升起一个巨大的锯片到高度 H，
并锯掉所有树比 H 高的部分（当然，树木不高于 H 米的部分保持不变）。Mirko 就得到树木被锯下的部分。例如，如果一排树的高度分别为
20,15,10 和 17，Mirko 把锯片升到 15 米的高度，切割后树木剩下的高度将是 15,15,10 和 15，而 Mirko 将从第 1 棵树得到 5 米，
从第 4 棵树得到 2米，共得到7米木材。

Mirko 非常关注生态保护，所以他不会砍掉过多的木材。这也是他尽可能高地设定伐木机锯片的原因。请帮助 Mirko 找到伐木机锯片的最大的整数高度H，
使得他能得到的木材至少为M米。换句话说，如果再升高 1 米，他将得不到 M 米木材。

输入格式

第 1 行 2 个整数 N 和 M，N 表示树木的数量，M 表示需要的木材总长度。

第 2 行 N 个整数表示每棵树的高度。

输出格式

1 个整数，表示锯片的最高高度。

思路：

和其他二分思路一样，这里的mid代表高度，让最低的高度为1，最高的高度为树的最大高度，每次循环判断，如果得到的树木长度大于M，
则向上继续移动，left = mid + 1；反之，right=mid-1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
using namespace std;
int n,m,l,r;
int a[1000005];
bool check(int x){   //答案是否满足，满足返回1，反之返回0
    long long int num=0;
    for (int i = 1; i <= n; i++){
        num += max(0,a[i] - x);
    }
    return num>=m;
}
void merge(){
	if(r-l<0) return;    //边界
	int mid=l+(r-l)/2;    //这样处理防止溢出
	if(check(mid)){   //如果满足，我们记录当前最大值，然后往右区间寻找答案
        l = mid +1;
		merge();
	}
	else{  //如果不满足，就往左区间寻找
        r = mid - 1;
		merge();
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
        r = max(r,a[i]);
	}
    l=0;
	merge();
	cout<<r;
    return 0;
}

关于二分查找的问题，就到这里，如果存在问题，请与我联系！